[Scikit-learn] 회귀 모델 성능 측정 지표 : MAE, MSE, RMSE, MAPE, MPE

회귀분석을 통해 예측 모델을 만들고 해당 모델의 성능을 파악하기 위해 사이킷런에서는 판단할 수 있는 지표 모듈이 있다.

 

# 선형 회귀모델(Linear Regression) 생성

사이킷런 라이브러리에 datasets 모듈을 생성한 후 당뇨병 데이터셋을 대상으로 선형회귀모델(Linear Regression)을 만든다.

# 1. 데이터셋 가져오기
data = datasets.load_diabetes() # 당뇨병 데이터셋 로딩
data.target

# 2. 데이터프레임 변환 후 합치기
df = pd.DataFrame(data.data, columns = data.feature_names) # 데이터셋 데이터 데이터프레임 변환
y = pd.DataFrame(data.target, columns = ['y']) # 데이터셋 타켓 데이터프레임 변환
df = pd.concat([df, y], axis = 1)

# 3. 데이터 스플릿
train, test = train_test_split(df, test_size=0.3, random_state=123)

# 4. 선형 회귀분석
from sklearn.linear_model import LinearRegression
LR = LinearRegression()
LR.fit(train.drop(columns = 'y'), train.y)
y_pred = LR.predict(test.drop(columns = 'y'))
y_test = test.y

---

1. MAE(Mean Absolute Error) : 평균절대오차

MAE

 

• 모델의 예측값과 실제값의 차이을 모두 더하는 개념이다.
• 절대값을 취하기 때문에 직관적으로 알 수 있는 지표다.
• MSE보다 특이치에 robust하다.(특이치에 영향을 많이 안 받는다는 의미다.)
• MAE는 절대값을 취하는 지표이기에 실제보다 낮은 값(underperformance)인지 큰 (overperformance)값인지 알 수 없다.

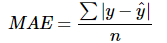
# 평균절대오차(MAE)
from sklearn.metrics import mean_absolute_error
mean_absolute_error(y_test, y_pred) # 44.48057319064366

---

2. MSE(Mean Squared Error) : 평균제곱오차

MSE

 

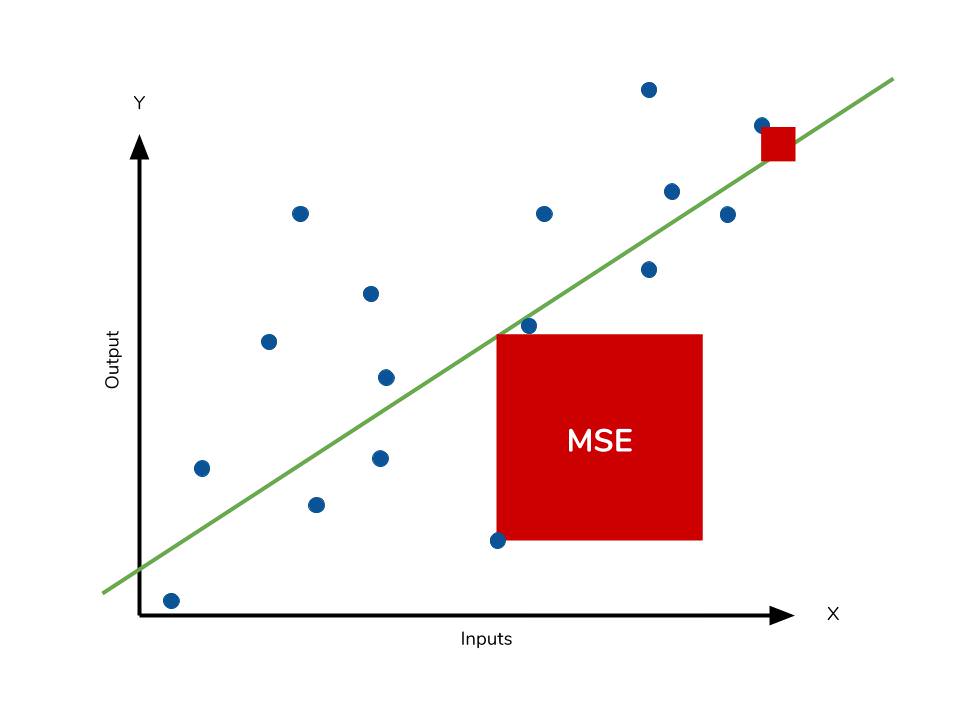
• MAE와는 다르게 제곱을 하기 때문에 모델의 실제값과 예측값의 차이의 면적의 합이다.
• 제곱을 하기 때문에 특이값이 존재하면 수치가 많이 늘어난다.( = 특이치에 민감함)

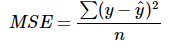
from sklearn.metrics import mean_squared_error
mean_squared_error(y_test, y_pred) # 2926.800577246883

---

3. RMSE(Root Mean Squared Error) : 평균 오차

• MSE를 구한 값에 루트를 씌운다.
• 오류 지표를 실제 값과 유사한 단위로 변환하여 해석을 쉽게 한다.

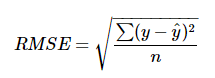
from sklearn.metrics import mean_squared_error
MSE = mean_squared_error(y_test, y_pred)
np.sqrt(MSE) # 54.09991291348705

---

4. MAPE(Mean Absolute Percentage Error) : 평균 절대 백분오차 비율

MAPE

 

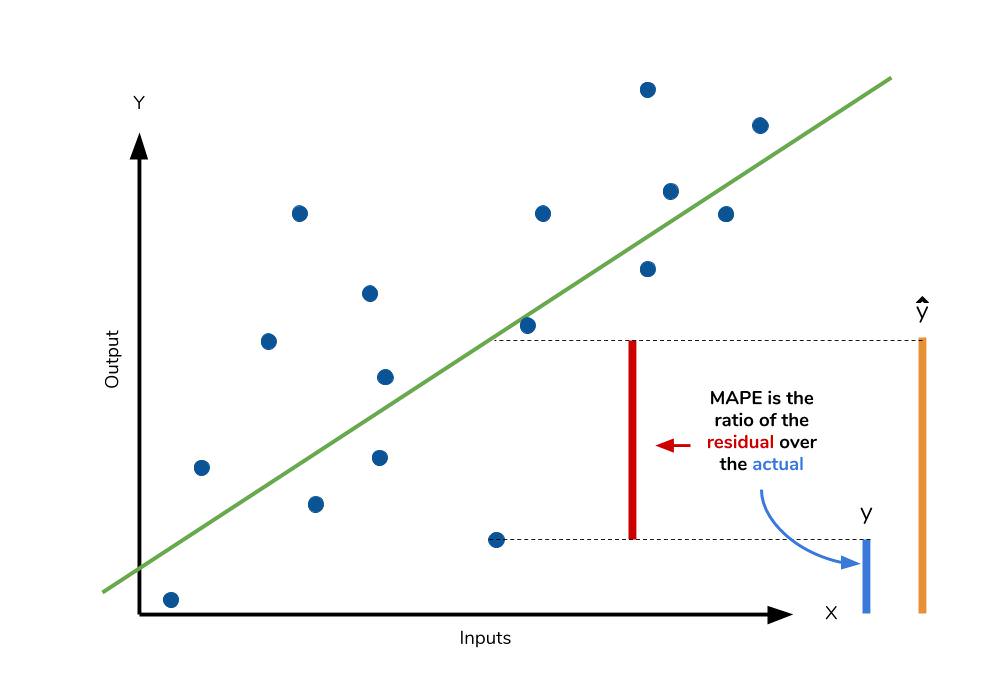
• MAE를 퍼센트로 변환한 것이다.
• MAE와 동일하게 MSE보다 특이치에 robust하며 실제값보다 낮은 값인지 높은 값인지 알 수 없다.
• 모델에 대한 편향이 있다.(이를 대응하기 위해 MPE도 추가로 확인하는 것을 추천)

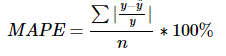
# 평균절대 백분오차 비율(MAPE)
def MAPE(y, pred):
    return np.mean((y-pred)/y * 100)

print(MAPE(y_test, y_pred)) # 39.726725527886714

---

5. MPE(Mean Percentage Error) : 평균 비율 오차

MPE

 

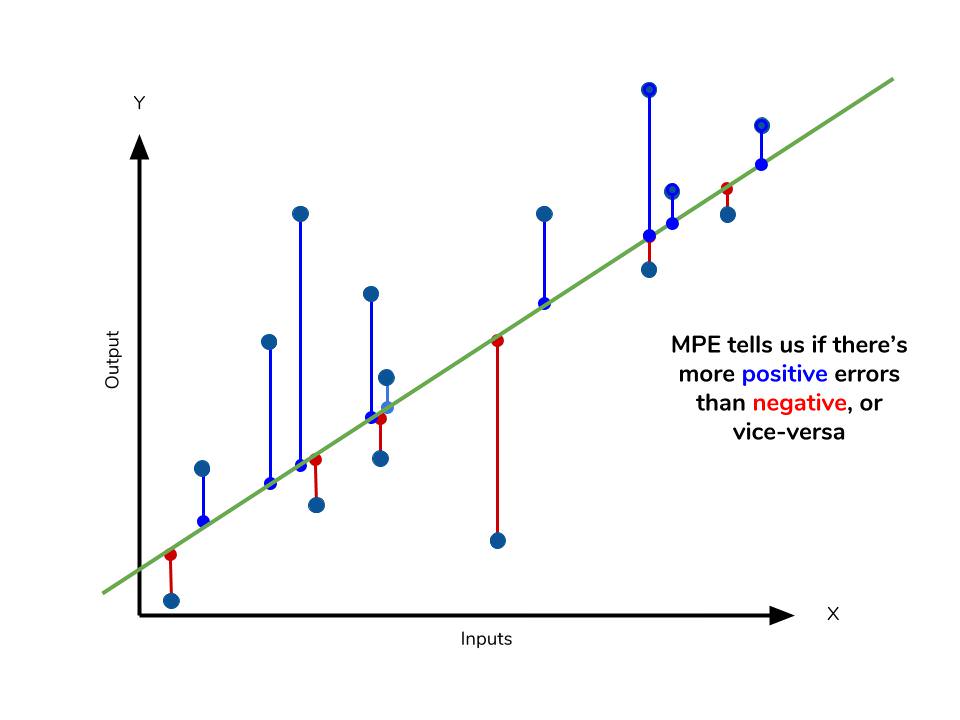
• MAPE와 비슷하지만 MAPE에서 절대값을 제외한 지표다.
• 장점은 모델이 실제값보다 낮은 값인지 큰 값인지 판단 할 수 있다.

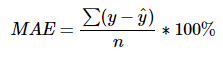
# 평균 비율 오차(MPE)
def MPE(y_true, y_pred):
    return np.mean((y_true - y_pred) / y_true) * 100
MPE(y_test, y_pred) # -19.399644435854015

---

 

다섯 가지 지표의 많은 특징들을 다루었지만, 모두 정확하게 기억하기에는 어려울 수 있다.

아래 테이블 표에서 기본 특성을 간략히 설명한다.

 

Acroynm (종류)	Full Name	Residual Operation? (잔차 계산)	Robust To Outliers? (이상치 영향)
MAE	Mean Absolute Error (평균절대오차)	Absolute Value (절대값)	Yes
MSE	Mean Squared Error (평균제곱오차)	Square (제곱값)	No
RMSE	Root Mean Squared Error (평균오차)	Square (제곱값)	No
MAPE	Mean Absolute Percentage Error (평균 절대 백분 오차 비율)	Absolute Value (절대값)	Yes
MPL	Mean Percentage Error (평균 비율 오차)	N/A	Yes

 

 

■ Reference

 

https://scikit-learn.org/stable/modules/model_evaluation.html#regression-metrics

3.3. Metrics and scoring: quantifying the quality of predictions

https://scikit-learn.org/stable/modules/classes.html?highlight=metrics#module-sklearn.metrics 

API Reference

https://www.dataquest.io/blog/understanding-regression-error-metrics/

Tutorial: Understanding Regression Error Metrics in Python